Acyclic joinの分類
はじめに
Acyclicなconjuntive queryにはいくつか定義があり、階層をなしています。 この記事では、論文を読む中で遭遇したある程度メジャーであると考えられるいくつかのクエリ種別についてまとめます。
$\alpha$-acyclic join
単にasyclic joinと呼ばれることもあります。 本記事で紹介するクエリ種別の中で最も広範なクエリを含む種別となっています。 conjunctive query $q(V, E)$は下記の条件を満たす木で構成された森が存在するとき、$\alpha$-acyclic joinとなります。
- 各リレーション$e \in E$を頂点とする
- 各変数$v \in V$について、$v$を含むリレーションのみを取り出したとき連結な部分木になっている
また、上記のような性質を持つ木をjoin treeと呼びます。
例を示します。 以下のクエリは画像のようなjoin tree $T$を構成することができるため、$\alpha$-acyclic joinです。 $$ \begin{align} V &= \{A, B, C, D, E, F\} \\ E &= \{(ABCD), (BCDE), (CE), (DE), (AF)\} \end{align} $$
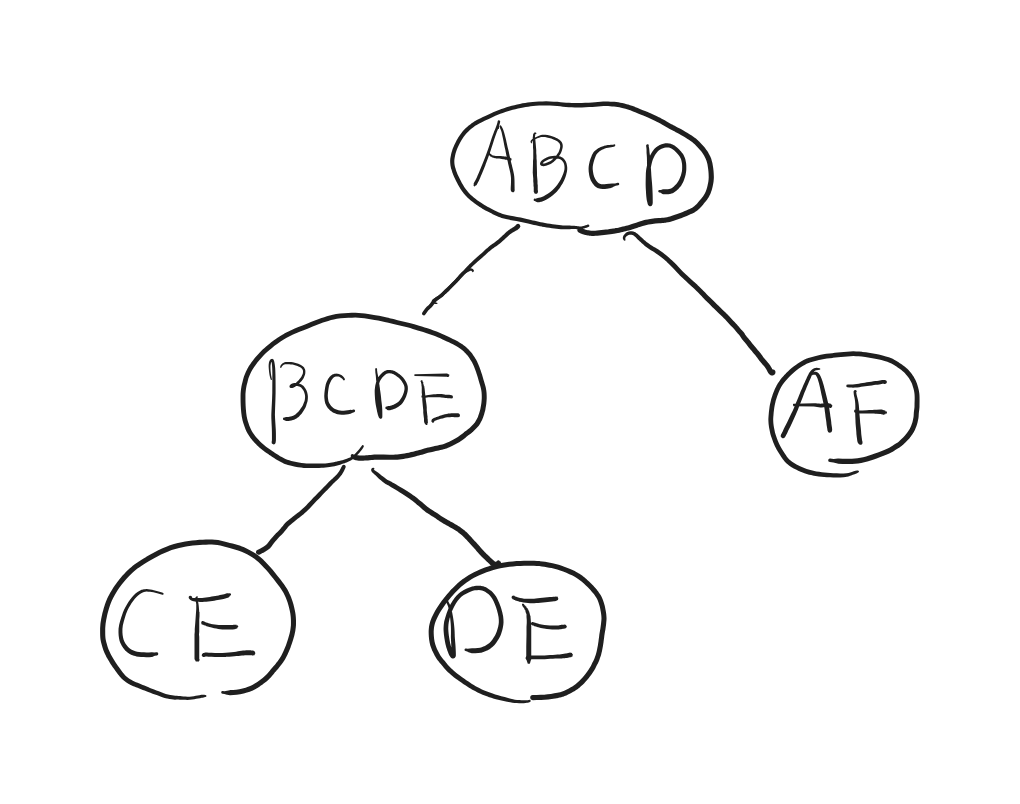
Hierarchical join
$E_x = \{e \in E\ : x \in e\}$としたとき(つまり、変数$x$を含むリレーションの集合)、任意の変数の対$x, y \in V$に対して以下の条件を満たすとき、conjunctive queryはhierarchical joinとなります。
- $E_x \subseteq E_y$
- もしくは$E_x \bigcap E_y = \emptyset$
hierarchical joinでは、$E_x \subseteq E_y$ならば$x$が$y$の子孫となるような森を構成することができます。
例を示します。
以下のクエリは、全ての変数のペア$(x, y)$について$E_x \subseteq E_y$もしくは$E_x \bigcap E_y = \emptyset$が成り立つため、hierarchical joinとなります。
$$
\begin{align}
V &= \{A, B, C, D, E, F\} \\
E &= \{(ABCD), (ABC), (AB), (AD), (EF), (E), (F)\}
\end{align}
$$
変数の森は以下の図の様になります。
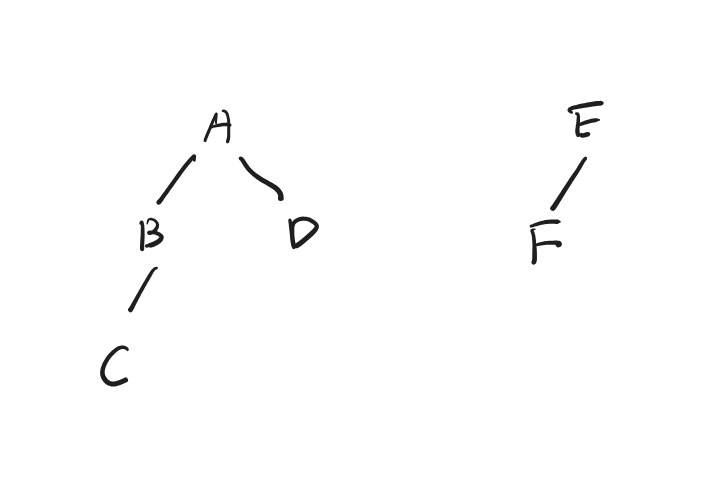このクラスのクエリはprobabilistic databasesやupdateが存在する状況でのクエリにおいて、良い特徴があるようです。
r-hierarchical join
r-hierarchical joinはhirarchical join拡張したクラスです。 具体的にはreduceという処理をクエリに対して実行したのちにhierarchical joinとなるクエリがr-hierarchical joinとなります。 reduceとは、あるリレーション$e \in E$に対して$e \subseteq e’$となるようなリレーション$e’ \in E$が存在する場合に、$e$を取り除く操作です。 reduceを繰り返し行い、これ以上reduceを行うことができなくなったクエリをreduced queryと呼びます。
例を示します。 以下のクエリは、変数のペア$(A, C)$に注目したとき、$E_A \bigcap E_C \neq \emptyset$であるのに$E_A \subseteq E_C$でも$E_C \subseteq E_A$でもないため、hierarchical joinではありません。 しかし、reduceを行うことでリレーション$BC$が削除されるためhierarchical joinとなります。 $$ \begin{align} V &= \{A, B, C\} \\ E &= \{(ABC), (AB), (BC)\} \end{align} $$ 上記のクエリをreduceすると以下のようになります。 $$ \begin{align} V &= \{A, B, C\} \\ E’ &= \{(ABC)\} \end{align} $$
Tall-flat join
Tall-flat joinは特殊なhierarchical joinです。 具体的には変数の集合$V = \{x_1, x_2, \dots, x_h, y_1, y_2, \dots, y_l\}$に対して、以下の条件が成り立つhierarchical joinがtall-flat joinとなります。
- $E_{x_1} \supseteq E_{x_2} \supseteq \dots \supseteq E_{x_h}$
- $j = [1, l]$について$E_{x_h} \supseteq E_{y_j}$
- $j = [1, l]$について$|E_{y_j}| = 1$
tall-flat joinの変数の森は以下の図のようになります。
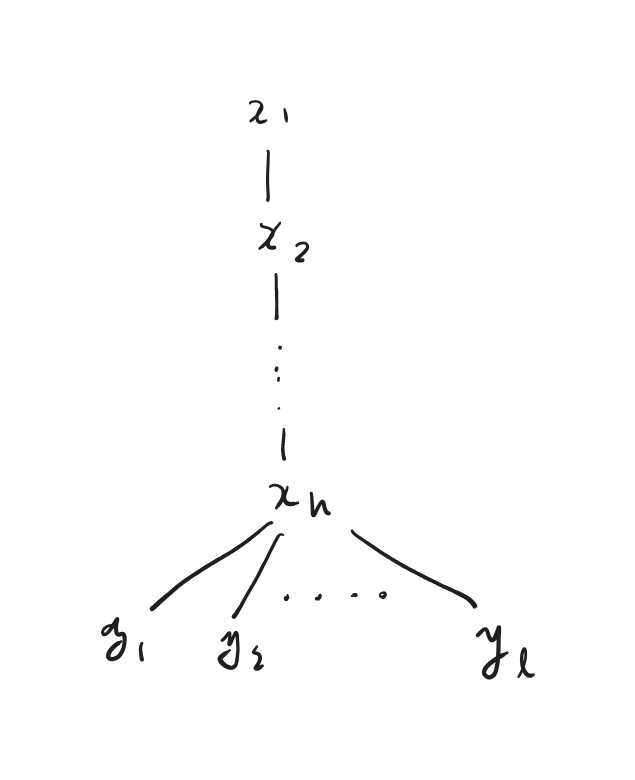一直線に並んだ$x$のパスの末端に$y$が連なる構造になります。
tall-flat joinの例としては以下のようなクエリが挙げられます。
$$
\begin{align}
V &= \{A, B, C, D, E, F\} \\
E &= \{(ABCD), (ABC), (AB), (A), (ABCDE), (ABCDF)\}
\end{align}
$$
変数の森は以下のようになります。
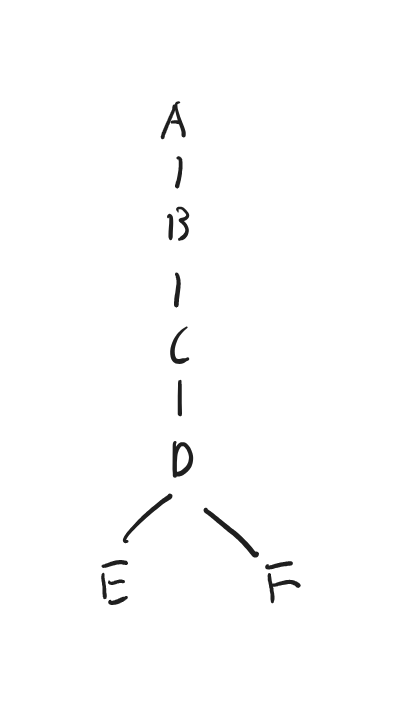
階層関係
最後に階層関係についてまとめます。
まず、定義よりtall-flat joinはhierarchical joinのサブクラスです。
また、hierachical joinはr-hierarchical joinです。
これは、reduceによって包含関係に変化が生じないためです。
例えば$E_x \subseteq E_y$という包含関係があった場合、$E_x$に含まれるリレーションは$x$と$y$を含みます。
この時、reduceによって$x$は含むが$y$を含まないリレーションが生まれると包含関係が崩れしてしまいますが、reduceの定義上リレーションが新しく生まれることはありません。
一方で、r-hierarchical joinはhierarchical joinではないクエリも含みます。
したがって、ここまでで以下の階層関係が成り立っていることが分かります。
$$
\begin{equation}
\text{tall-flat} \subseteq \text{hierarchical} \subseteq \text{r-hierarchical}
\end{equation}
$$
次にr-hierarchical joinとacyclic joinの関係について考えます。
もしr-hierarchical joinの中にacyclic joinに含まれないクエリが存在したとします。
この場合、このクエリのjoin treeを構成しようとすると閉路が生まれてしまうことを意味しています。
閉路が生まれてしまうということは、互いに素ではなくかつ包含関係にない変数のペアが存在することになります。
例えば、$(AB), (BC), (CA)$というリレーションが存在する場合、join treeを構成しようとすると閉路になってしまい、$E_A$と$E_B$は互いに素ではなくかつ包含関係にもありません。
また、reduceによってこの閉路を解消しようとすると、閉路に含まれる全ての変数を含むリレーションが必要になりますが、そのようなリレーションが存在する場合、そもそも閉路を含まずにjoin treeを構成することができます。
例えば、先ほどの例の場合$(ABC)$というリレーションがあると、reduced queryでは閉路を解消することができますが、そもそも下記のようなjoin treeが構成できるため、前提条件に合致しません。
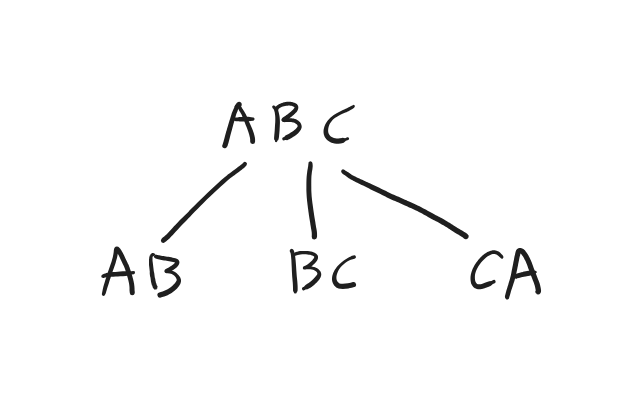したがって、r-hierarchical joinは必ずacyclic joinとなります。
以上より、最終的な階層関係は以下のようになります。
$$
\begin{equation}
\text{tall-flat} \subseteq \text{hierarchical} \subseteq \text{r-hierarchical} \subseteq \text{acyclic}
\end{equation}
$$